2.競馬における統計分析の基礎

KeibaAiNavi

統計学を用いた競馬データの分析方法

TARGETを用いて、過去のレースデータを入手することが可能ですが、どのように各ファクターがレース結果与える影響を分析すればいいか。

特に重要となるのが、確率の偏りを補正してあげることです。

過去のデータの中には、様々な条件や特別な状況で発生した結果のデータがいくつもあるため、きれいな直線や曲線ではなく凸凹なグラフになっています。

そのようなデータを統計学に基づいた方法で補正をすることで、正しく傾向を読み取ることが可能となります。

単一ファクターによる分析

1つのファクターに焦点を当てた場合、そのファクターが回収率にどのような影響を与えるかを分析してみましょう。

具体例として、ダートレースにおける枠番毎の回収率を見てみます。

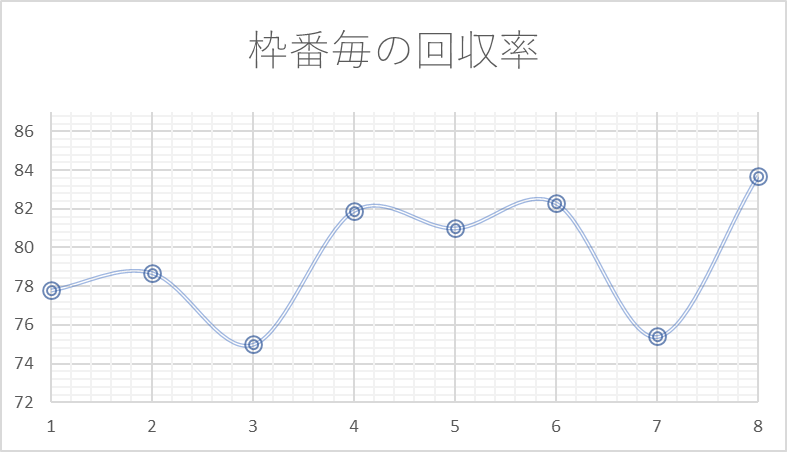
ダートレースでは一般的に、外枠有利と言われています。理由は主に次の通りです。

内枠の馬は、前の馬の蹴り上げる砂(キックバック)を受け戦意を喪失することがある
スタート直後は、スピードが出やすい芝を走るコースが多く、外枠のほうが芝を走る距離が長い

実際にデータでも外枠に行くにしたがって回収率が上がっているように見えますが、3枠や7枠の回収率が下がっており、凸凹になっています。

しかし、外枠有利の理屈を考えても7枠が6枠よりも不利となる理由はないため、確率の偏りにより、偶然7枠の回収率が低い結果となった可能性が高いと考えられます。

そのような確率のばらつきを補正し、全体の傾向を把握するために、回帰分析と呼ばれる統計学に基づいた分析を行います。

回帰分析とは

回帰分析は、統計学を用いて様々なファクターと結果との関係を分析する方法です。

競馬での回収率の分析においては、レースの様々な要素が回収率にどのように影響するかを解明するために用いることが可能です。

まずは、実際に回帰分析を行った結果を見てみましょう。

グラフの赤線が回帰分析の結果です。元データの値を平らにならしたグラフとなっています。

これにより、確率の偏りにより生じた凸凹を補正し、各ファクターが回収率にどのような影響を与えているか、視覚的にも理解できるようになります。

線形と非線形

ダートレースの枠番に関する分析結果では、回帰分析の結果は直線でした。

しかし、分析するファクターによっては直線とは異なる形を示すこともあります。

次のグラフは人気順毎の回収率をグラフ化したものです。

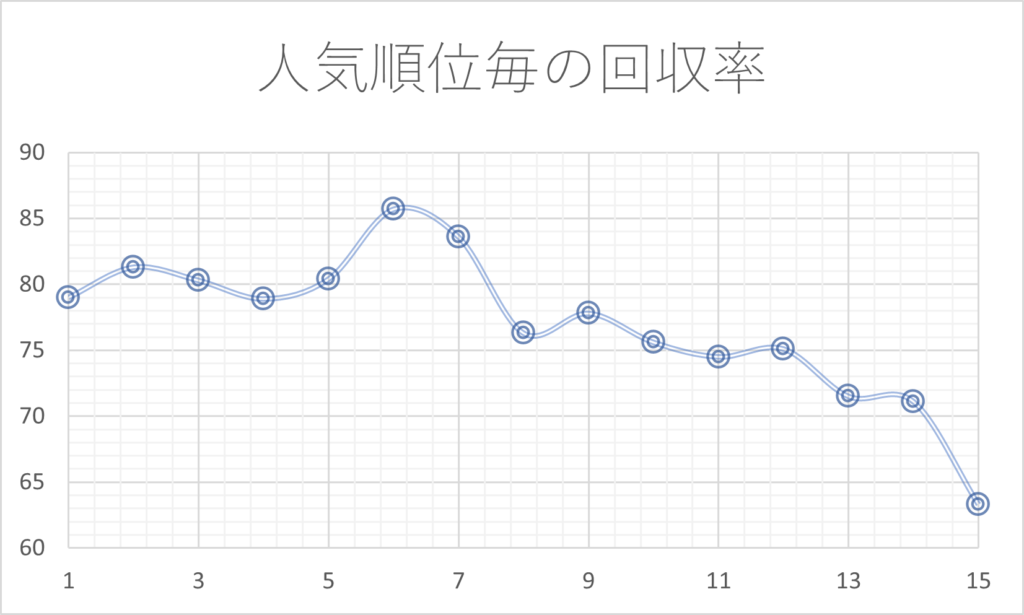
人気上位の馬は能力が高いため、オッズが過剰に下がることが多く、また極端な人気薄の馬も高配当狙いのために実力以上にオッズが下がります。そのため、直線的な傾向ではなく、カーブを描くような傾向となっていると予測できます。

人気順毎の回収率について回帰分析を行った結果が次のグラフです。

5番人気～6番人気あたりが最も回収率が高くなっています。

先程の枠番では直線、つまり1次関数であったのに対し、人気順では2次関数型になっているのがわかります。

このように、ファクターによって適切な次数を見極める必要があります。

複数ファクターによる分析

複数のファクターを含むモデルでは、それぞれのファクターが回収率にどのように影響するかを分析する必要があります。

ここでダートレースにおける馬場の含水率毎の枠位置別回収率を調べてみましょう。

次のグラフは、回収率が高い範囲を赤で、低い範囲を青で表したヒートマップです。

含水率が低い、つまり良馬場のときは外枠が有利になっています。

一方で含水率が高い、つまり重馬場のときは内枠が有利となっています。

ダートレースでは外枠は芝を長く走れ、また内枠はキックバックの影響を受けやすいため、一般に外枠有利と言われてはいます。

しかし、重馬場になることでダートコースでもスピードに乗ることができ、またキックバックも軽減されるため、距離ロスが少ない内枠が有利になると推察できます。

ここで、「含水率」と「枠」という2つのファクターを基にして回帰分析を行い、ヒートマップで表してみます。

先ほどのヒートマップと比べて、平準化されました。
これにより視覚的にも内枠が有利となる場合、外枠が有利となる場合についての傾向を理解しやすくなっています。

回帰分析を行うことで確率の偏りによる凸凹をならし、回収率が高くなる範囲、低くなる範囲を適切に理解することが可能になります。

分析に必要なデータ数は1万件以上

分析結果の精度を高めるためには、十分なデータ量が必要です。

特に、競馬のレースは最大18頭の競走馬が出走しますが、単勝馬券で言うと対象になるのは1頭だけです。

このような場合、データのばらつきが大きくなるため、競馬では一般的な統計データと比べても多くのデータが必要となります。

必要なデータ数はファクターによっても変わってくるため、一概に何件以上あれば十分とは言えず経験則に基づく数値となりますが、少なくとも５千件～１万件のデータは必要と考えてください。

データ量が増えれば、統計的な信頼性が向上し、データ内の様々なパターンや関係性をより詳細に分析できます。

逆に言うと、少ないデータを基にした分析は、統計学的な観点からは適切とは言えません。

よくWebなどで見かける「有馬記念過去10年の枠別データ」などは、多くても180頭分のデータです。データ数が足りていない場合、枠毎の有利不利よりも確率の偏りの方が結果に大きく影響します。

単純な枠番別の結果ではなく、各年の出走馬の能力を考慮した上で適切に脳内で補正ができるのであれば問題ありませんが、結果のみを切り取るとただ偶然の結果を並べただけの数値となっています。そのようなデータは、信頼度が著しく乏しいと言えます。

未来のレースに対する有効性

ここまで分析してきたデータはあくまでも過去のデータです。過去のデータから、未来のレースでも有効な傾向を読み取るためには次の2つの観点を意識して分析することが必要です。

分析時の注意点：必要以上に過去のデータに合わせようとしない
分析後の確認点：疑似的に未来のデータで検証を行う

①分析時の注意点：必要以上に過去のデータに合わせようとしない

データ分析を行う上で最も注意しなくてはならないことの1つが過剰最適化です。

分析対象のデータに対して高い回収率となるように追求しすぎた結果、未来のデータに対して大きくパフォーマンスを落としてしまうことを「過剰最適化」言います。

例えば、回帰分析の説明の中で、人気順毎の回収率の分析において2次関数での分析を行いましたが、これを3次、4次、5次…と次数を上げたものが次のグラフです。

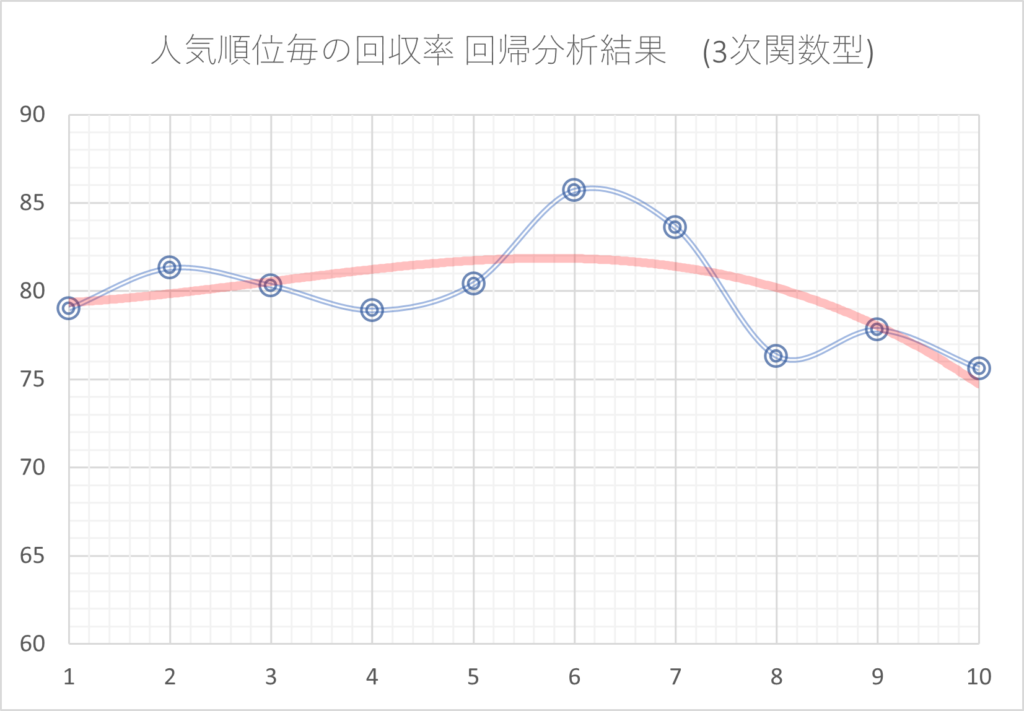
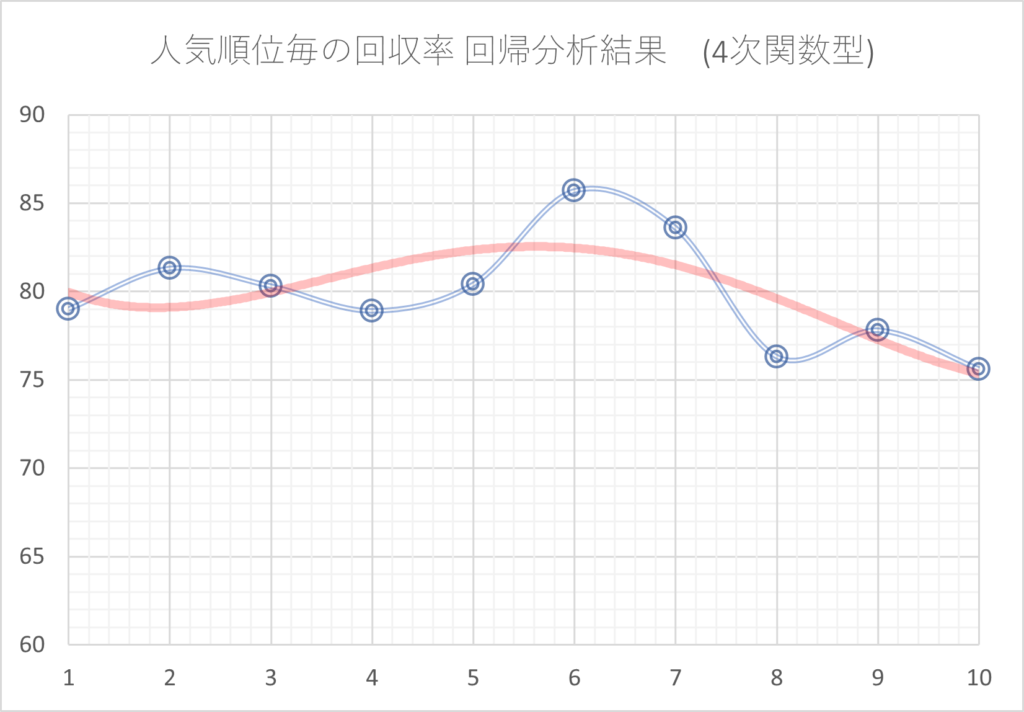
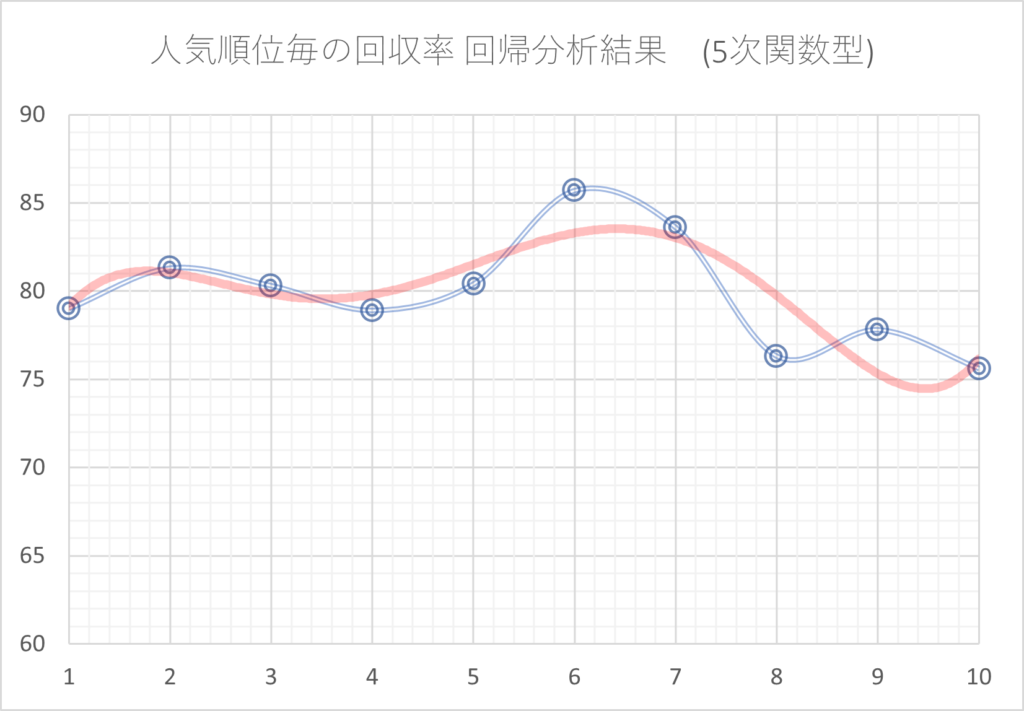
次数を大きくすればするほど、元のデータに近づいています。しかし、これは言い換えると、元のデータと同じく多くの凸凹がある結果となっているということです。

このように、元のデータとの差を小さくするために複雑な分析を行いすぎると、過去の確率のばらつきまで再現してしまいます。その結果、未来のデータに対しては分析結果通りにならないことが多くなります。

一般的に、次数を上げる、多くのファクターを同時に掛け合わせる、というように分析を複雑化すればするほど過剰最適化になりやすくなります。

回帰分析を行う際には極力、1次関数型(直線)または2次関数型(山なり)とするようにしてください。

3次関数以上を採用する場合については、そのような形状となる理由を論理的に説明できる状況に限定するべきです。

②分析後の確認点：疑似的に未来のデータで検証を行う

分析結果が過剰最適化となっていないかを確認する方法としては、フォワードテストというものが有効です。

フォワードテストとは、未来のデータが過去のデータの分析結果と合致しているかを確認する方法です。しかし当然ながら、未来のデータを用意することはできません。そのため、擬似的に未来のデータに対する有効性を検証する方法を説明します。

例えば5年分のデータが存在するとします。ここでデータを次の2つに分割します。

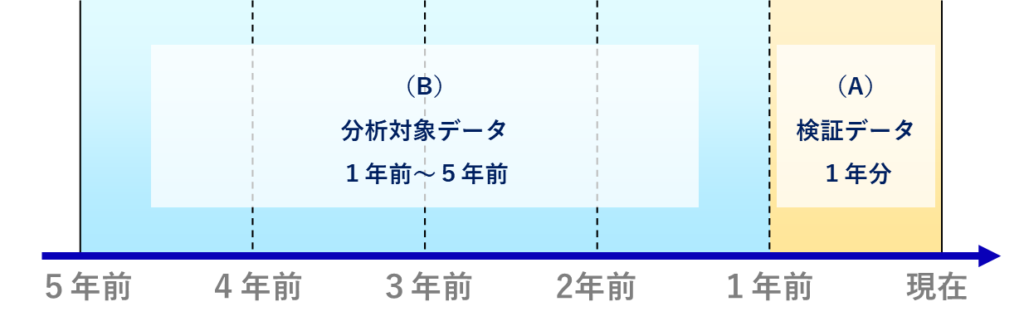
直近の1年間分のデータ……(A)
2年前〜5年前までの4年間分のデータ……(B)

(B)の過去データから見ると、(A)の直近データは未来のデータとなります。ここで、(A)の直近データは使用せず、(B)の過去データのみを使って分析を行います。

その後、(A)の検証データのみを使用して分析を行い、過去データと同様の傾向が見られるかを確認します。

(A)の検証結果が、(B)の分析結果と大きく異なる場合、その内容は未来のデータに対して有効性は低いデータであると考えられます。

過剰最適化を回避しつつ、フォワードテストを行うことで、未来のレースに対しても有効な分析を行いましょう！

「統計分析の基礎」

重点解説記事はこちら

回帰分析の基本と分析方法

ABOUT ME