回帰分析の基本と分析方法

回帰分析とはファクターが回収率に与える影響の予測
回帰分析は、統計学において、データ間の関係性を数学的に表現する方法です。
競馬のデータ分析においては、特定のファクター(独立変数)が回収率や勝率など(従属変数)にどのような影響を与えているかを予測するために使用します。
分析の結果は式やグラフで表すことができます。この式を用いてファクターの値毎の期待値を予測することができます。
具体例を見てみましょう。
.png)
こちらの青色のグラフは実際の過去データの値を示しています。しかし、当然ながら様々な偶然的要因によってきれいな直線や曲線にはならず、凸凹なグラフになっています。
回帰分析を行うことにより、その凸凹をなくし傾向をわかりやすくしたものが赤い直線です。
用語解説
回帰分析を行うにあたり使用する基本的な用語から、分析結果等で目にする用語のうち、主なものまとめました。
最初からすべての用語を理解する必要はありませんが、分析を行う中でわからない単語が出てきた際に確認してみてください。
- 用語解説
-
- 独立変数(説明変数):
分析の対象となる現象や結果に影響を与えると考えられる変数。例えば、枠番、馬場状態、前走着順の経験など。 - 従属変数(目的変数):
独立変数の影響を受ける、分析の目標となる変数。このサイトでは主に回収率。 - 回帰係数:
独立変数の一単位の変化が従属変数にどれだけの影響を与えるかを示す係数。
Y=aX+bの式で言えば”a”にあたる数値。 - 切片:
回帰線がy軸と交差する点。独立変数がすべてゼロの場合の従属変数の予測値。
Y=aX+bの式で言えば”b”にあたる数値。 - R2(決定係数):
回帰モデルがどれだけデータに適合しているかを示す指標。
0から1の範囲で、1に近いほど良い適合度。0に近いほど、ファクターと期待値の関係性が薄いことを意味する。 - 相関係数:
二つの変数間の線形関係の強さを示す値。
-1から1の範囲で、-1は完全な負の線形関係(反比例)、1は完全な正の線形関係(正比例)を示す。 - 多重共線性:
複数のファクターを用いた分析を行う際に、そのファクター同士に強い相関関係がある状況。これにより、回帰分析の結果が不安定になることがある。 - 標準誤差:
回帰係数の推定の精度を示す値。小さいほど、推定値が真の値に近いことを示す。 - p値:
統計的仮説検定で使用される値。小さいp値(通常は0.05以下)は、その結果が偶然である可能性が低いことを示す。 - 残差:
実際の観測値と回帰モデルによる予測値との差。残差分析はモデルの適切性を評価するのに使われる。 - 異常値(外れ値):
他の観測値から大きく逸脱しているデータポイント。外れ値は分析結果に大きな影響を与える可能性がある。 - 信頼区間:
回帰係数の真の値が存在すると推定される範囲。通常、95%の信頼区間が使用される。 - 対数変換:
線形でない関係を線形に近づけるために、変数に対して対数変換を行うこと。これにより、モデルの適合度が向上することがある。 - F統計量:
モデル全体が統計的に有意かどうかを評価するために使用される値。F統計量が大きいほど、モデルは統計的に有意。 - 交互作用項:
二つ以上の独立変数が組み合わさって従属変数に影響を与える際に用いられる。
Y=aX1+bX2+cX1X2 の式で言えば”cX1X2”にあたる項。 - 非線形回帰:
従属変数と独立変数間の関係が非線形である場合に適用される回帰分析手法。
- 独立変数(説明変数):
これらの用語をはじめとして、基礎知識や基本概念を理解することで、精度が高い回帰分析を行うことが可能となります。
Excelを利用した分析方法

実際に回帰分析を行う方法についてはさまざまありますが、その中でも特別な知識がなくとも簡単にできる方法を中心にご紹介します。
Excelを用いた簡単な回帰分析方法
Excelで作成したグラフに、回帰分析グラフや数式を追加する方法を紹介します。
※Excelのバージョン等により、若干手順が異なる可能性があります。
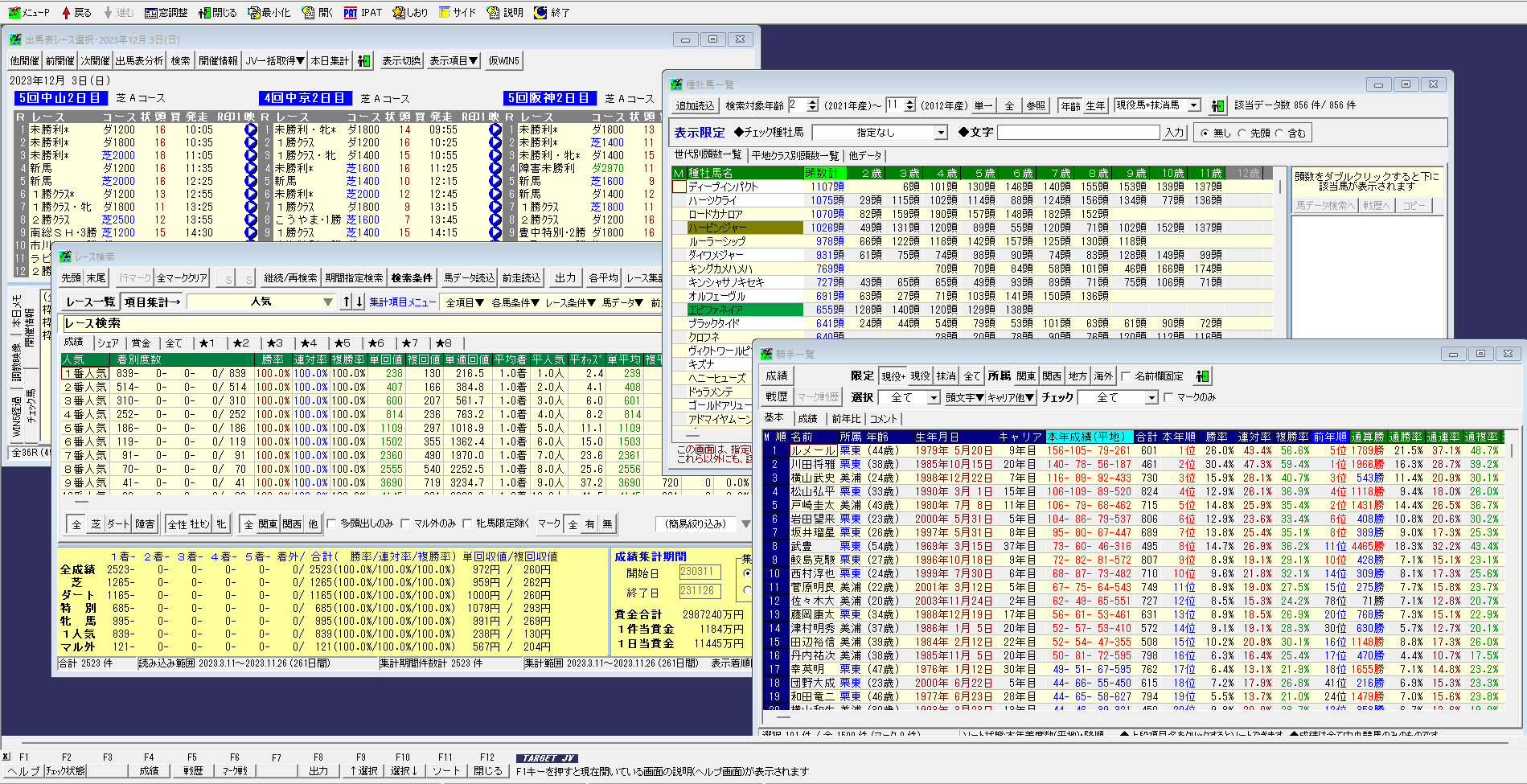
TARGETで分析したいファクターを調べます。ここではダートレースの枠番別成績を調べてみます。
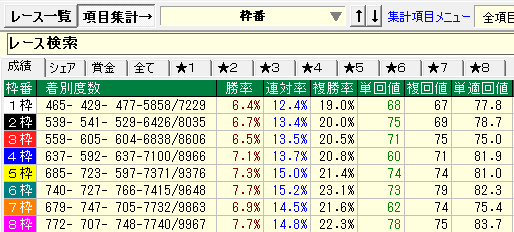
先ほどの結果をExcelに貼り付け、折れ線グラフ化します。
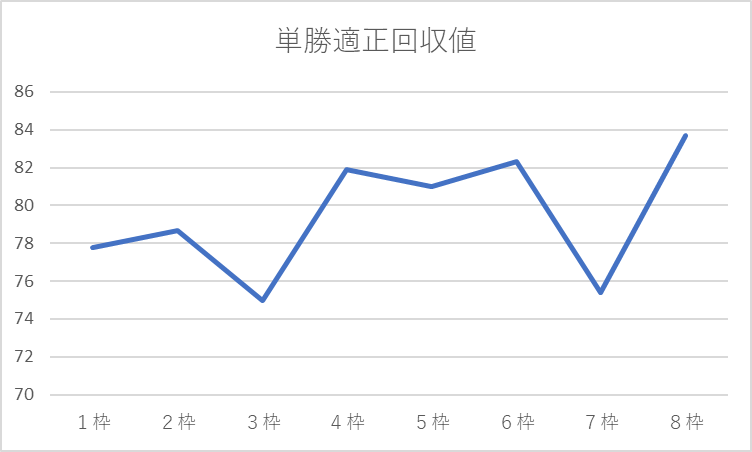
グラフ右上に表示される「+」マークにマウスを合わせ、表示される一覧の中から「近似曲線」にチェックを入れる
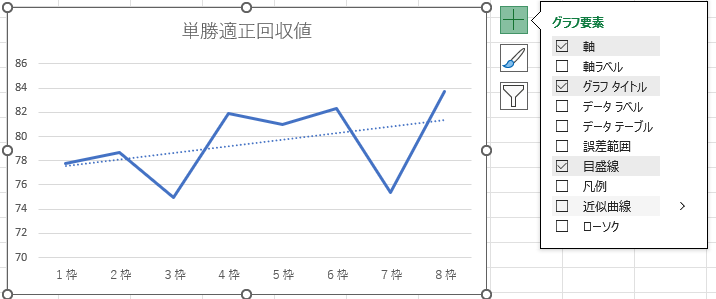
新たな点線がグラフに追加されます。これが直線(線形)の回帰分析結果結果となります。
新たに表示された点線部分をダブルクリックすると、Excel右側に「近似曲線の書式設定」が表示されます。
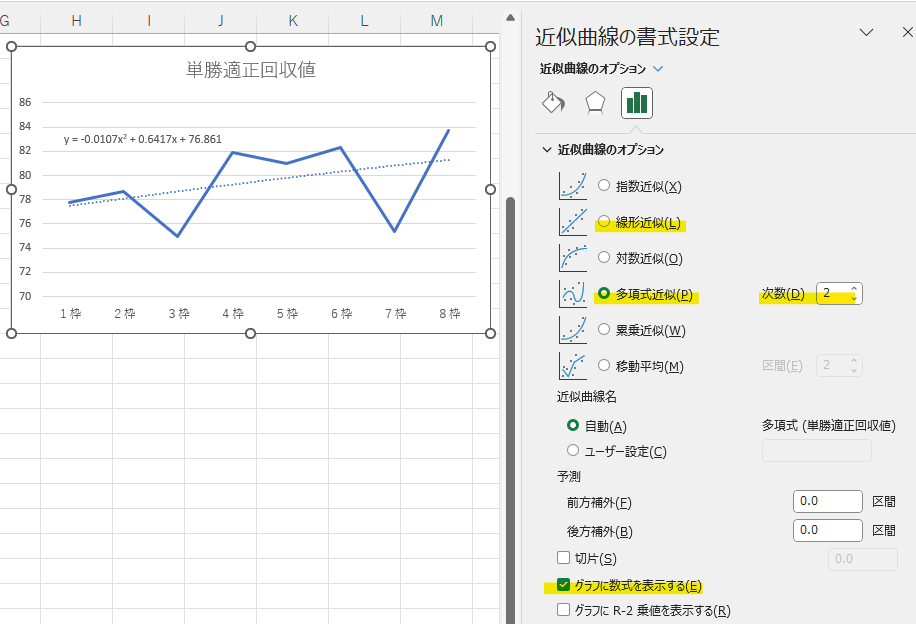
ここで「多項式近似」を選択することで、2次以上の関数型の近似曲線へ変更できます。直線が最も適している場合は「線形近似」を選択します。
どの次数が最も適しているか、次数を変更しながら確認してください。
また、下部にある「グラフに数式を表示する」にチェックを入れることで、回帰分析の結果を数式で表示することができます。
このように、Excelで非常に簡単に回帰分析を行うことができます。しかし、この方法には次のようなデメリットがあります。
各データ母数による重み付けや複数ファクターを掛け合わせた分析(多重回帰分析)を行うためには、より専門的な機能を使用する必要があります。その方法については別記事で解説します。
異常値を除去することで回帰分析の精度を向上させる
回帰分析の精度を上げるためには、事前の加工処理が必須となります。
特に、データの分母数が少ないものは、確率の偏りにより極端に高い(低い)回収率となっていることがあります。そのデータをそのまま使用してしまうと、ファクターごとの傾向を正確に捉えることができなくなってしまいます。
そのため、分析前にあらかじめ異常値を除去することが必要です。
異常値の除去
こちらは、芝のレースにおける、人気順ごとの回収率をグラフ化したものです。
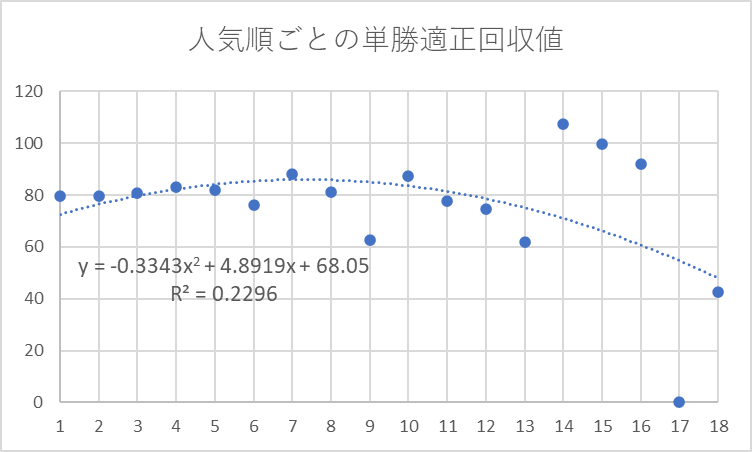
14番人気から16番人気は回収率100%前後と高くなっておりますが、一転して17番人気は回収率0%と極端に低くなっています。
これは、レースによって出走頭数が異なるため、下位の人気順になるほどデータの母数が少ないことが原因にあると想定できます。
ここで、14番人気以下を異常値として除外し分析してみます。
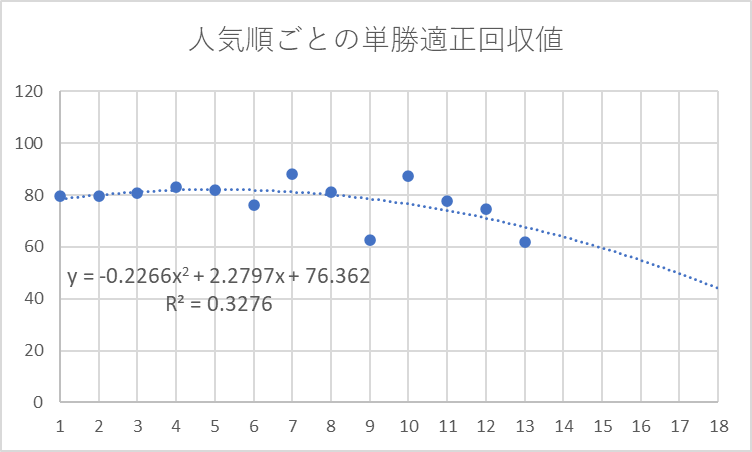
異常値を除去することで、上位人気馬の値についても、より適切に評価できるように見受けられます。
R2(決定係数)についても、0.2296から0.3276と上昇しており、よりファクターが回収率を適切に説明できているということを示しています。
このように、異常な値となっているデータを分析対象から除去することで、分析の精度を上げることが可能となります。
どのような値を異常値と考えるか
異常値を除去するにあたって、「どのような値であれば異常値とみなすか」を決める必要があります。統計学的にも異常値判断の方法は複数存在しますが、競馬の分析においては以下の2パターンのからの選択で問題ないと考えます。
- 回収率の絶対値を基にした判断
- 分散値を基にした信頼区間内外での判断
回収率の絶対値を基にした判断
こちらは単純に、一定の値以上・以下の回収率となっているデータを除去するという判断です。
その値の設定をどの程度にするかは個々人の判断により異なってきます。
しかし、十分な母数があるデータにおいては、1つのファクターで回収率100%を超えるということはほぼありません。そのため、私の場合は回収率60%以下、100%以上は基本的に異常値としてとらえています。
分散値を基にした信頼区間内外での判断
こちらはより統計学的アプローチによる判断となります。
データの分布が正規分布であるという仮定の下、加重平均からどの程度乖離しているかを基準として異常値を判定します。
- 加重平均の計算
データの平均値を計算します。この際に各データポイントの重みを考慮します。 - 標準偏差の計算
データの標準偏差を計算します。
標準偏差は、データが平均値からどれだけ散らばっているかを示す数値です。 - 3σルールの適用
「±3σ」とは、平均値からプラスマイナス3倍の標準偏差の範囲を意味します。
この範囲を超えるデータポイントは、異常値(外れ値)と見なされます。
つまり、データが平均からかなり離れている場合(平均 ± 3倍の標準偏差よりも大きいまたは小さい場合)に、そのデータポイントは異常であると判断し、分析から除外します。
なお、3σの場合は全データのうち約0.27%を異常値と判断します。2σとした場合は約4.55%を異常値と判断することとなります。
絶対値を基にした判断と比べると、専門的であり、また計算処理が必要となるため、難易度が高い方法となります。
回帰分析は過去データを適切に評価する統計学的方法
統計学に基づいて、様々なファクターを回帰分析することにより、期待値を数値化することが可能となります。
いきなり専門的な分析を行うのではなく、まずはExcelの「近似曲線」を作成する機能を使用することで、専門的な知識がなくとも簡単に分析を行うことを推奨します。
その際、あらかじめ異常値となるデータを除去することで、分析の精度が向上します。異常値の判定方法はいくつか存在しますが、まずは一定の値以上(以下)のデータを除外するという方法でも十分に分析精度の向上が見込めます。
こうした分析により、過去のデータを適切に評価し、各馬の指数算出に活用しましょう。